Notes on Merge sort
February 24, 2022
Some basic notes about Merge Sort algorithm.
Description
Recursive algorithm based on the divide and conquer strategy. It has two main components:
- A function that splits the a list recursively until it receives a single item.
- A «merge» function that merges two already sorted lists into a combined sorted one.
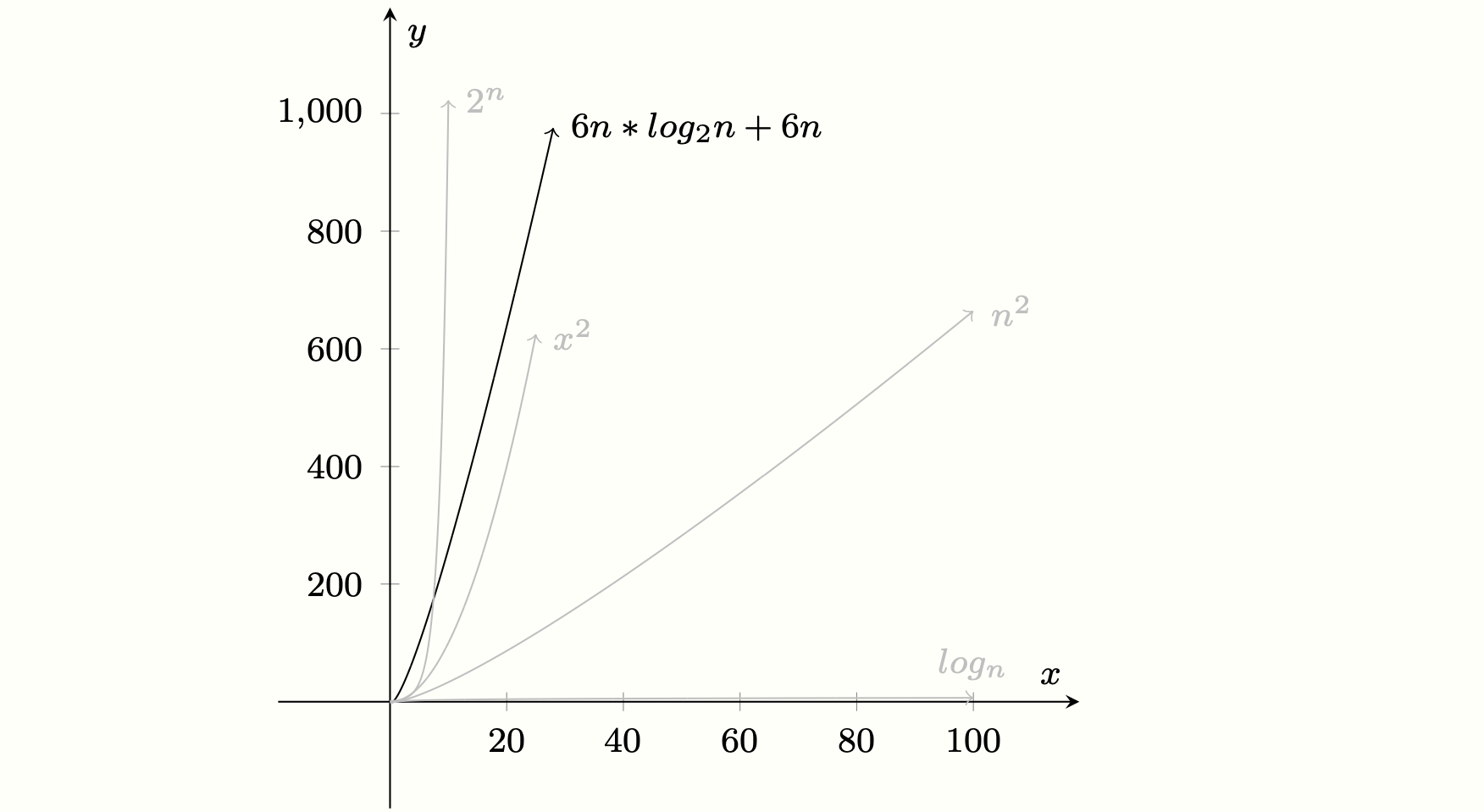
Time complexity
Pseudocode
Input: A = [A_1, A_2, …, A_n];\\Output: B = [B_1, B_2, …, B_n];\\[10pt]function \enspace MergeSort(A)\\\quad n \leftarrow length(A);\\\quad if \space n \leqslant then:\\\quad\quad return \space A;\\\quad else:\\\quad\quad l \leftarrow [A_1, …, A_{n/2}];\\\quad\quad r \leftarrow [A_{(n/2)+1}, …, A_n];\\\quad\quad L \leftarrow MergeSort(l);\\\quad\quad R \leftarrow MergeSort(r);\\\quad\quad B \leftarrow Merge(L, R);\\\quad\quad return \space B;\\\quad end \space if;\\end \space function;\\[10pt]function Merge(L, R)\\\quad n \leftarrow length(L) + length(R);\\\quad B \leftarrow [\space];\\\quad i \leftarrow 0;\\\quad j \leftarrow 0;\\\quad for \space k \leftarrow 0 \space to \space n \space do:\\\qquad if \space i \leqslant length(L) \space and \space j \leqslant length(R) \space then:\\\qquad\quad if \space L[i] \leqslant R[j] \space then:\\\qquad\qquad B[k] \leftarrow L[i];\\\qquad\qquad i \leftarrow i + 1;\\\qquad\quad else \space if \space L[i] \text{\textgreater} R[j] \space then:\\\qquad\qquad B[k] \leftarrow R[j];\\\qquad\qquad j \leftarrow j + 1;\\\qquad\quad end \space if;\\\qquad else \space if \space i + 1 \leqslant length(L) \space then:\\\qquad\quad B[k] \leftarrow L[i];\\\qquad\quad i \leftarrow i + 1;\\\qquad else \space if \space j + 1 \leqslant length(R) \space then:\\\qquad\quad B[k] \leftarrow R[j];\\\qquad\quad j \leftarrow j + 1;\\\qquad end \space if;\\\quad end \space for;\\\quad return \space B;\\end \space function;
Implementation in Rust
language-rust
pub fn merge_sorted_arrays(left: Vec<i32>, right: Vec<i32>) -> Vec<i32> {
let left_length = left.len();
let right_length = right.len();
// Final array will be the size of both provided arrays
let mut sorted_items = vec![0; left_length + right_length];
let mut i = 0;
let mut j = 0;
// Iterate over the array that we will fill with items either
// in left or right arrays
for k in 0..sorted_items.len() {
// If neither "i" and "j" pointers did reach the limit
// of their respective arrays
if i + 1 <= left.len() && j + 1 <= right.len() {
// Decide between current item in left array and current item
// in right array which one will be next in final array
if left[i] <= right[j] {
sorted_items[k] = left[i];
i = i + 1;
} else if left[i] > right[j] {
sorted_items[k] = right[j];
j = j + 1;
}
} else if i + 1 <= left.len() {
// If only "i" pointer didnt reach the limit —but "j" did—
sorted_items[k] = left[i];
i = i + 1;
} else if j + 1 <= right.len() {
// If only "j" pointer didnt reach the limit —but "i" did—
sorted_items[k] = right[j];
j = j + 1;
}
}
sorted_items
}
pub fn sort_array(unsorted_array: &Vec<i32>) -> Vec<i32> {
let n = unsorted_array.len();
if n <= 1 {
// Base case: if input has length of one it is already sorted,
// return it
let sorted_array = unsorted_array.to_vec();
sorted_array
} else {
// If input has length bigger than two, then:println!
// 1. Split it
let (left, right) = unsorted_array.split_at(n / 2);
let left_vec = left.to_vec();
let right_vec = right.to_vec();
// 2. Sort it recursively
let left_sorted = sort_array(&left_vec);
let right_sorted = sort_array(&right_vec);
let sorted_array_1 = merge_sorted_arrays(left_sorted, right_sorted);
sorted_array_1
}
}
fn main() {
let unsorted_array: Vec<i32> = vec![2, 1, 4, 3];
let sorted_array = sort_array(&unsorted_array);
println!("unsorted_array: {:?}", unsorted_array);
println!("sorted_array: {:?}", sorted_array);
}
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn works_with_sorted_arrays() {
let unsorted_array = vec![1, 2];
let sorted_array = sort_array(&unsorted_array);
let expected_result = vec![1, 2];
assert_eq!(expected_result, sorted_array);
}
#[test]
fn works_with_simple_unsorted_array() {
let unsorted_array = vec![2, 1];
let sorted_array = sort_array(&unsorted_array);
let expected_result = vec![1, 2];
assert_eq!(expected_result, sorted_array);
}
#[test]
fn works_with_simple_uneven_lenght_arrays() {
let unsorted_array = vec![2, 1, 3];
let sorted_array = sort_array(&unsorted_array);
let expected_result = vec![1, 2, 3];
assert_eq!(expected_result, sorted_array);
}
#[test]
fn it_works_with_sorted_arrays() {
let left = vec![1, 2];
let right = vec![3, 4];
let merged = merge_sorted_arrays(left, right);
let expected_result = vec![1, 2, 3, 4];
assert_eq!(expected_result, merged);
}
#[test]
fn it_works_with_splits() {
let left = vec![3, 4];
let right = vec![1, 2];
let merged = merge_sorted_arrays(left, right);
let expected_result = vec![1, 2, 3, 4];
assert_eq!(expected_result, merged);
}
#[test]
fn it_works_with_uneven_length_lists() {
let left = vec![3, 4, 5];
let right = vec![1, 2];
let merged = merge_sorted_arrays(left, right);
let expected_result = vec![1, 2, 3, 4, 5];
assert_eq!(expected_result, merged);
}
#[test]
fn it_works_with_single_item_lists() {
let left = vec![3];
let right = vec![1];
let merged = merge_sorted_arrays(left, right);
let expected_result = vec![1, 3];
assert_eq!(expected_result, merged);
}
}